Computing the probability of winning any peg game
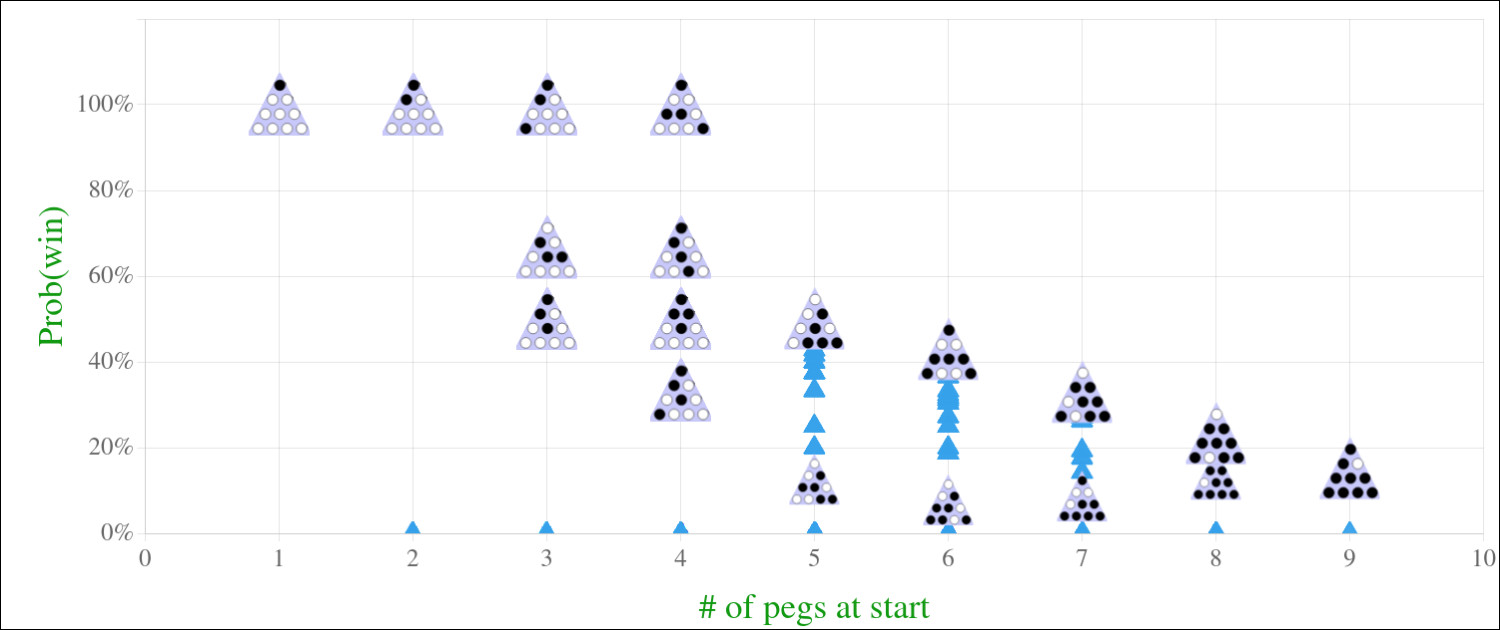
I created a program to solve peg games and also compute a probability of winning from any position. A lot of the code is available at this Replit if you want more details or to make any modifications.
The Rules
The rules for the variation I will be solving:
- Move in any of 6 directions.
- Jump over one peg to an unoccupied spot and remove the peg that was jumped over.
- Repeat until there are no more legal moves.
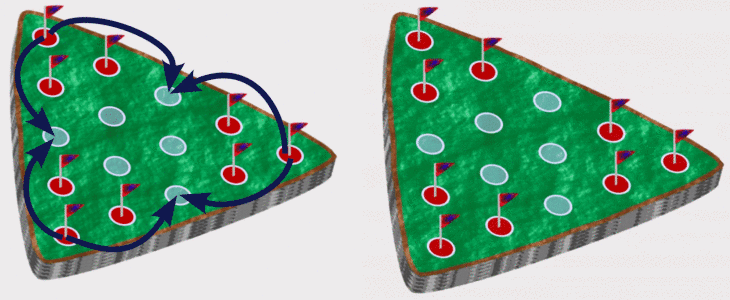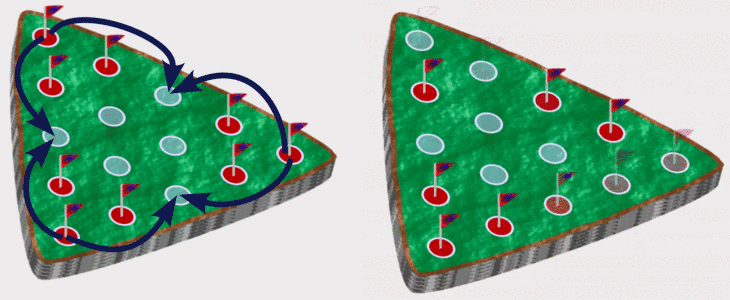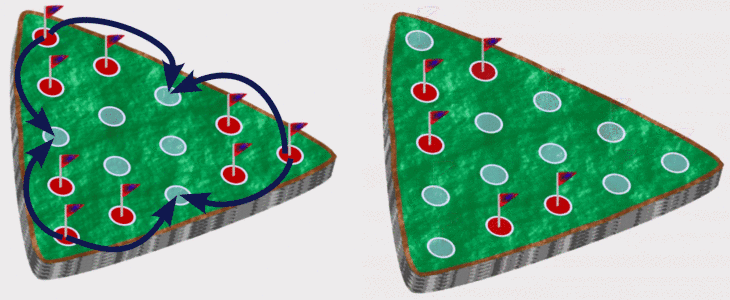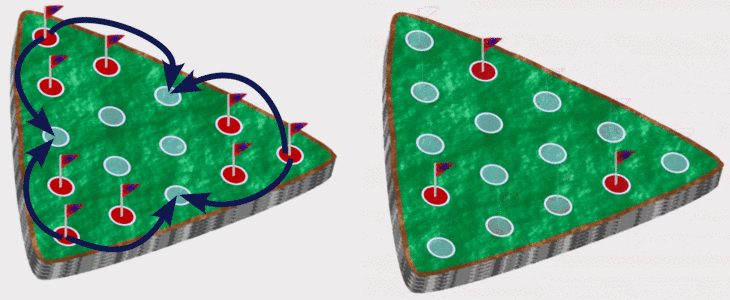
The goal is to end with as few pegs remaining on the board as possible, and a winning outcome is one peg left. A standard game starts with a triangular arrangement of 15 holes with one peg missing, but any starting arrangement can be solved with the same methods.
Probability
What is the probability of winning a game? Each human is different so there is not one exact answer. Even assuming someone plays randomly there are still (at least) two reasonable choices for how to define the probability.
One way is to assume that each move is random so if there are 2 legal moves, then each has probability of 50%. We can multiply the probabilities at each step and compute a probability of reaching each terminal position (no more legal moves). Then to compute the probability of ending with 1 peg we add up the probabilities of all winning positions.
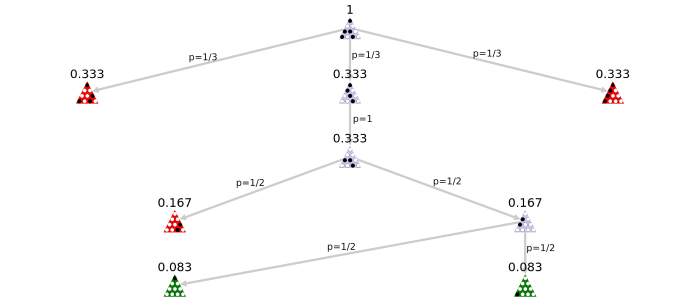
In the above game, there are two winning positions (in green) and three losing positions (in red) but the losing positions have much higher probabilities so there is only a 1/12 chance of winning if each move is randomly decided.
Another method is to compute the set of all unique games, where a game is a full series of moves ending at a terminal position. Then simply determine the percentage of these games that are wins. In the above example, there are five unique games (there are five terminal positions and each has a unique set of moves to reach it) with just two winning games so the probability of winning is 2/5.
The second method generally has higher probabilities for winning positions. Losing games are shorter so each losing position tends to have a higher probability when using the first method since it is the product of fewer factors.
Humans will be better than random in some situations and mostly try to avoid repeating losing moves, so I will use the second method. I just need a fast way to compute the number of unique games, which grows exponentially as the number of starting pegs increases.
Alternative Methods to Solve
Before discussing the algorithm I used, I want to mention some nice alternatives.
The simplest option is to randomly make moves. There are only a handful of legal moves each turn so running 10,000 simulations takes almost no time and provides a pretty accurate estimate of the likelihood of winning. Aside from being inexact, this method requires rerunning simulations for each initial position.
A better option is either a breadth-first or depth-first algorithm to iterate all of the paths. If you enjoy recursion or wish to learn, I encourage you to try to write a program to find all possible games. But I am going to avoid recursion since it is not necessary in this scenario.
Creating a Graph
I am going to create a graph where each node represents a possible arrangement of pegs. Then for each node, I will determine all legal moves and add an edge to each position that results.
Each hole can either have a peg or not, so there are a total of nodes (including positions that are not possible) where n is the number of holes in the game. I can take advantage of this fact to give each node a unique name that is a binary string with a 1 in each place where there is a peg.
For puzzles with up to about 25 holes (33,554,432 nodes) everything should be plenty fast. To make reasonable visualizations for this post, I am going to focus on a board with just 10 holes in a triangular arrangement.
The graph below includes every possible game that starts with just one peg missing in the middle-right of the bottom row. The starting position is at the top, each row has one fewer peg, and if you look closely you can see that each edge represents a valid move.
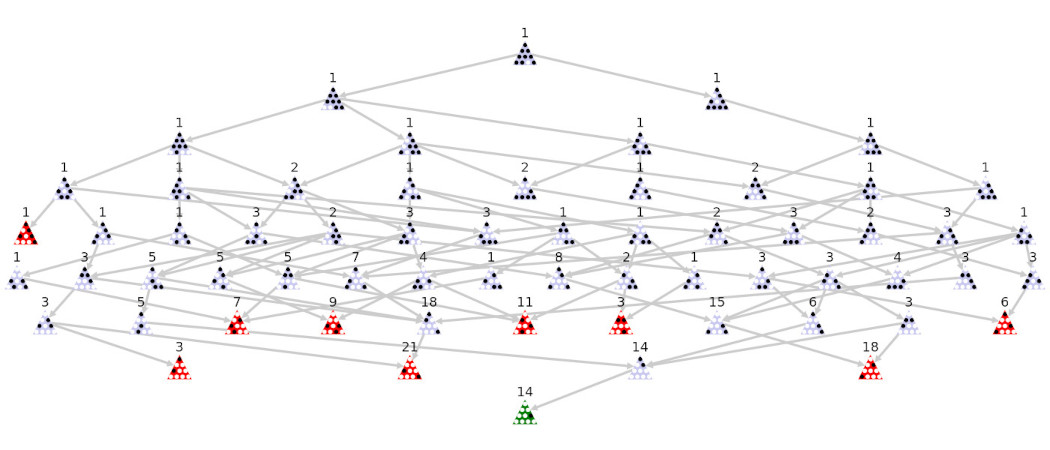
The number above each node is the number of unique sets of moves that reach that node. For the first few rows we see that there is only one way to reach each position, but then some positions can be reached multiple ways and it is quite simple to compute the number of unique paths.
For each node, find all of the arrows pointing to it and add up the numbers above the previous positions. This approach is a variation of this problem. After computing all of these numbers I can add up the winning games, add up all of the games, and then divide.
There is only 1 winning position above (shown in green at the bottom) and there are 14 unique ways to get there. There are 9 losing positions (shown in red) with a total of 79 unique ways to lose. Therefore the probability of winning from that starting position is .
This method only determines the probabilities for the one starting position. Instead of repeating this approach each time, I will work from the bottom up to get all of probabilities in one run.
Reversing the Graph
I will create a similar graph as above but start with the terminal positions. The edges connect the same node pairs as before but they point in the opposite direction.
The initial nodes will be all of the winning positions and then the graph will connect the nodes until hopefully reaching a position with just one peg missing. After using the same method of counting the answers will all be 14 (each starting position that is winnable happens to be a rotation/mirror of the others).
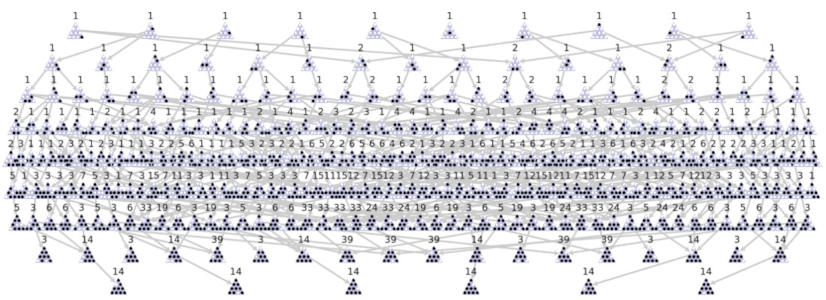
There are 6 starting positions that are winnable and each reaches exactly one possible winning position in 14 unique ways. If I repeat this process but starting with all terminal positions with 2 pegs left, the result is 42 possible games for each of the 6 starts. Repeating with all terminal positions the result is the same 93 as above so the probability of winning is the same: about 15%.
Some positions with more than 1 peg missing have more than 14 winning games so those positions are likely easier. However, some positions only have 1 winning path so they could be harder even though more pegs are missing initially.
Wrapping Up
The counting process is the slowest part but only needs to be done once. Once all of numbers have been crunched, it is fast to compute the win probability from any position.
Each node requires a few bytes of storage for the counts so for 15 holes all the data compresses down to a reasonable 170 KB. But the growth is exponential so 25 holes requires more than 200 MB.
As the table below shows, the relative difficulty of a position is hard to predict (which is why these puzzles are challenging). Computing these probabilities is therefore a big help for creating challenges of a certain difficulty, helping players identify which moves were bad ideas, or quickly offering hints/solutions.
| Start | 1 peg | 2 pegs | 3 pegs | 4+ pegs |
|---|---|---|---|---|
 | 1550 (1.12%) | 20686 (15.01%) | 62736 (45.51%) | 52874 (38.36%) |
 | 442.29M (12.71%) | 948.49M (27.26%) | 1.37B (39.25%) | 723.17M (20.78%) |
 | 8.61B (7.95%) | 21.87B (20.21%) | 48.17B (44.52%) | 29.56B (27.32%) |
 | 215 (30.07%) | 206 (28.81%) | 236 (33.01%) | 58 (8.11%) |
 | 195 (1.77%) | 1674 (15.24%) | 5361 (48.8%) | 3756 (34.19%) |
Visit my Replit if you want to see the code, modify any code, or just play. If you want more of a challenge, try to write your own code to solve with different algorithms or languages.
To play more varieties/shapes and track your progress, visit Qblur where I also sell handcrafted epoxy resin peg games in several shapes like watermelons and U.S. states.