Postfixing More Math Expressions
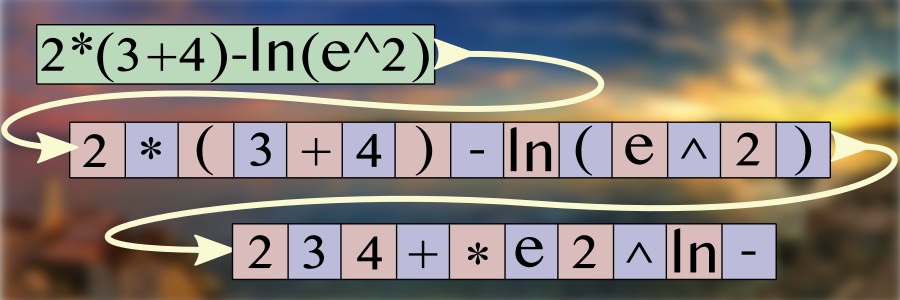
Basics of Postfix Notation
For background, read the earlier post on how to postfix simple expressions if you haven't already. The goal is to turn an infix math expression like into an array like 31215+*+4-
. The operands remain in order while the operators are interspersed exactly where they need to be to follow the correct order of operations.
In this post we will add more operations and see how the algorithm needs to be adjusted to make things work. Converting a wide range of typical math expressions is possible with a relatively short algorithm.
With many edge cases there are several correct options. Details about where the input is coming from and what happens to the output will influence which choices are better. For now, I will do what seems simplest and/or most obvious. I will assume that the input has proper syntax so there will not be any implied multiplications (like 3x meaning 3*x) to worry about.
Parentheses
Anything inside of parentheses needs to be performed separately before the surrounding outside operations, but even multiple nested parentheses are easy to order properly with just a few lines of code.
When creating the infix array, we will treat parentheses just like operators. Opening and closing parentheses will each have their own element in the array.
When creating the postfix array, we will always add an opening parenthesis to the stack. When we reach a closing parenthesis, clear the stack until an opening parenthesis is hit and remove that parenthesis entirely. The parentheses will never be part of the postfix array.
else if (infixArray[i] =="(") {stack.push(infixArray[i]); } else if (infixArray[i] == ")") {while (stack[stack.length-1] != "("){postfix.push(stack[stack.length-1]);stack.pop();}stack.pop();//to remove the "(" from the stack }
Exponentiation
Exponentiation needs a higher precedence than multiplication or division, but most important is to treat exponentiation as right associative. The other arithmetic operations are left associative so operations are performed left to right when precedence is equal. As an example, because we subtract 5 from 8 first rather than subtracting 2 from 5.
Exponents are performed right to left. Thus 2^3^4 is the same as instead of . To deal with this difference we will have to check for consecutive exponents when the precedence of the last operation in the stack matches the precedence of the new operation. The new operation is the rightmost exponent so it gets pushed to the stack like any higher precedence operation.
else if (prec[stack[stack.length-1]] == prec[infixArray[i]] && infixArray[i] == "^){ stack.push(infixArray[i]); }
Factorial
The factorial operation is actually already in postfix notation because the operator comes immediately after the operand. When creating the infix array, treat ! as an operator so that it is separated from the operand. When creating the postfix array, treat ! as an operand and just push it to the postfix array.
else if (infixArray[i] =="!"){postfix.push(infixArray[i]); }
Spaces
For the most part, whitespace can be ignored because it is between an operand and an operator like in 2 + 3 = 5. It is important to properly handle the space in something 3! = 6 to avoid confusion with 3 != 6, though.
We will deal with spaces when creating the infix array. Create a new element in the array, but don't add the space.
else if (input[i] == " "){if (arr[arr.length-1] != ""){arr.push("");} }
Multi-character Operations
Some operations use more than one character. Comparisons like "<=" should occupy one element in the infix array. For now, every multi-character operation has "=" as the second character so we will just check for that.
if (i+1<input.length && input[i+1] == "="){if ("!<>=".indexOf(input[i]) > -1){arr.push(input[i]+input[i+1]);arr.push("");i++;//we want to skip the next char since it's been handled} }
Functions
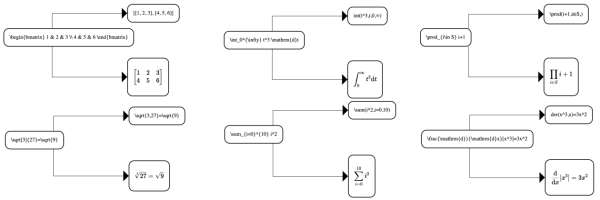
Trigonometric functions like sin(x) can be handled easily by just adding "sin" to the precedence map. The entire word will be added to one element in the infix array automatically. The entire input should be inside of parentheses so giving these functions high precedence will put them immediately after the correct operand.
For now we will only worry about a defined subset of all possible functions. Determining whether an arbitrary string is a function name or a variety of other options will be a task saved for later.
Logarithms
The natural log function can be treated just like sin(x), and different bases are also simple if we require that logarithms be defined as log_{b}(x). This syntax works surprisingly well by treating {} the same as () and discarding the "_".
The log ends up getting added to the postfix array after both the {b} and (x), which is exactly where it should be. Functions before parentheses stay in the stack no matter how many sets of parentheses are chained afterwards.
When evaluating we will need to know how many inputs each operator takes. The "ln" operator will always take one input and the "log" operator will always take two (the base and what's inside the log).
Comma Separated Inputs
Some functions (max, min, sum) might have an unknown number of inputs that are separated by commas inside of parentheses. We will define a comma operation with low precedence. There are other options like limiting the max and min functions to two inputs, but our approach creates something like an array when concatenating the comma operations.
Negative Numbers
We are going to divide the "-" operator into three cases. In an expression like we want the "-" to be part of the negative number "-2". In an expression like we want the "-" to be represent the subtraction operation. In an expression like we want the "-" to represent the negation operation.
It is critical to know how many inputs each operator acts upon, and negation only acts on one input while subtraction acts on two. When creating the infix array, we will either push a "-" to represent subtraction or "0-" to represent negation.
If it the first character in the expression, it is a negation. If it immediately follows an opening parenthesis, a comma, or most operators, it is a negation. The main exception is the factorial.
else if (input[i] == "-"){if (str.length > 0){arr.push(str);}if (i == 0){arr.push("0-");} else if (arr.length > 0 && prec[arr[arr.length-1]] > 0){arr.push("0-"); } else {arr.push(input[i]); } str = ""; }
When creating the postfix array, subtraction will be treated like any other operator but negation will sometimes be simplified as a negative number. When the negation operator is moved to the postfix array we will check the preceding element in the postfix array.
If it is a number (integer or decimal), we will place a negative at the front instead of creating a new element with the "0-" operator. There is nothing wrong with just using the negation operator, but most people think of -4 as simply a number rather than the number 4 and the negation operator.
The "0-" operator should always just be added to the stack because it is a unary operator (acting on just one input). Once it is part of the stack it should have lower precedence than exponentiation so that -4^2 evaluates to the generally accepted answer of instead of . I think the correct precedence is to match it with multiplication since negation is equivalent to multiplying by -1.
This approach correctly deals with potential issues like -4*-3, -(4+2)*-x , -4+-3, and even -4--3.
Full Algorithm
Visit Replit to see and interact with the code. I have also created repls in Python, C++, bash, and blockly if you want to use those languages. There could be bugs and differences between the algorithms, but they should help get you started.
The postfixing step is part of a larger collection of parsing functions that powers mathzetta.com. I will be posting more about the preceding steps soon.
Demo
Enter an expression below to see the postfixed output.